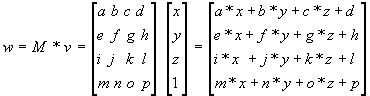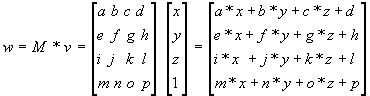Class Name: Local 4X4
Definition
A sixteen element matrix used to scale, orient, and position objects in the
scope of its parent LSR Transformation.
The direction of rotation is
determined by the right-hand rule. The translation parameters are always in
the rightmost column of the matrix.
Since a Local 4X4 only occurs as part of an
LSR Transformation, and an
LSR Transformation only occurs in
the scope of an LSR spatial reference frame, the objects to which a
Local 4X4 is applied are always defined in
an LSR spatial reference frame. (Since LSR spatial reference frames are
usually used to define Models but not
Environment Roots,
Local 4X4 is usually considered to be 'local'.
However, an Environment Root may be
defined in an LSR spatial reference frame, in which case
LSR Transformations would be legal
within its scope.)
The matrix multiplication order is defined by w = M * v, where M is the
Local 4X4 matrix, v is the original location
vector, and w is the resulting location vector.
Primary Page in DRM Diagram:
Example
- The position and orientation of the control tower in a
Model of
an airport is specified by the Local 4X4.
See Transformation for more examples.
FAQs
- How is the transformation matrix stored?
- SEDRIS stores matrices in row major order; that is, the
first four elements correspond to the first row of the matrix, the
following four elements correspond to the second row of the matrix,
and so on (just as a float[4][4] in C is organized). Hence, if
mat[][] is the matrix being used, then mat[i][j] is the element in
row i and column j of the matrix.
- What is the multiplication order for
Local 4X4 matrices?
- If M is a Local 4X4 transformation
matrix and v is a column location vector, then the SEDRIS Level
0 API transforms v to a column location vector w by setting w = Mv.
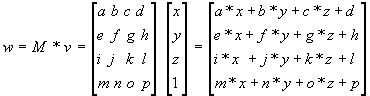
- Is a matrix in SEDRIS the same as a matrix in OpenGL?
- No. A matrix in SEDRIS is stored in row major order, while in OpenGL,
matrices are specified in column major order (as in the glMultMatrix
function). Consequently, to correctly apply SEDRIS transformations in
OpenGL programs, each matrix must be reordered.
Constraints
None.
Component of (one-way)
Notes
Fields Notes
A standard 4X4 transformation matrix
Prev: Lobe Data.
Next: Location.
Up:Index.